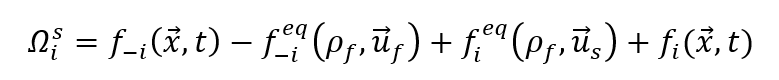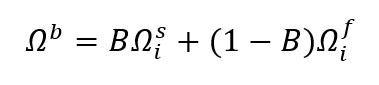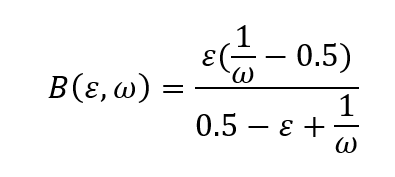Research Summary Report of B03

[17.03.2023]

K. Kutscher (PostDoc), kutscher@irmb.tu-bs.de

M. Geier (PI), geier@irmb.tu-bs.de

M. Krafczyk (PI), kraft@irmb.tu-bs.de

TU Braunschweig, IRMB

The primary aim of the project is to understand and quantify the dynamic distribution of material components (fluid, air and particles) and kinetic energy inside the jet of liquid concrete present in the shotcrete process. The information is required as a basis for future optimization of the process with regards to process and material parameters as well as for the prediction of material inhomogeneities.

Summary

For the modeling of the shotcrete process, the project currently proceeds with the development of several model components. The coupling between the lattice Boltzmann method for fluid flow and the Discrete Element Method for solid aggregates has been implemented and validated.

The large density and viscosity contrast between the cement paste and surrounding air remains to be the primary challenge for the simulation of the turbulent jet in the shotcrete process. Despite the progress in phase field modelling of the two-phase flow using the split distribution approach, the diffuse interface treatment common to state-of-the-art phase field models is still not stable enough for the full-scale simulation of the shotcrete process. In order to circumvent the difficulties arising from the large gradients in density at the diffuse interface we are now developing a sharp interface approach where the interaction between the phases is modelled through boundary conditions. Sharp interface models for the lattice Boltzmann methods have been in use as free surface models neglecting the air phase altogether. Since neglecting the air phase is not an option in our application, we modified the ansatz in the following way: The air phase is fully considered and coupled to the liquid phase via a velocity boundary condition. The liquid phase is coupled to the air phase via a pressure boundary condition as usual in a free-surface model, yet, unlike in these models the pressure is locally determined from the momentum balance between the air and the liquid phase. The location of the interface is identified through a contour of the phase field. The latter is not possible in a free surface model as it requires the knowledge of the velocity in the air phase. We are hence combining the simplicity of the phase field approach from diffuse interphase models with the robustness of the free surface approach to a sharp interface phase field method.

Current state of research

The coupling of the DEM (Discrete Element Method) particle solver LIGGGHTS to our CLBM solver VirtualFluids was implemented to incorporate the simulation of the fluid-structure interaction between the grains and the fluid(s). Within VirtualFluids, the integrated momentum acting from the fluid(s) onto each solid particle is computed and communicated to the particle solver as a force and a torque acting on the particles. The incorporation of the particles into the lattice Boltzmann solver was implemented by the immersed boundary method using a distributed force field. The nodes across the fluid-particle boundary build a boundary cell. The collision operator Ω becomes dependent on the local solid fraction ε (1 in solid, 0 in fluid, 0<ε<1 in a boundary cell). If the solid fraction ε is zero, the regular collision operator Ω_f is used. The non-equilibrium bounce-back introduced by Noble et al. is used to calculate a solid collision operator Ω_s for ε=1.

For nodes on the boundary with 0<ε<1, the collision operator becomes

where B is a weighting function related to the solid fraction and the relaxation rate.

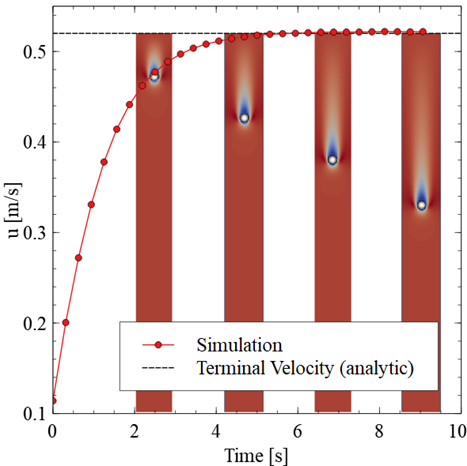
Fig. 1 demonstrates the accuracy of the immersed boundary method with a falling sphere benchmark. The theoretical terminal velocity is captured with an error of less than 1.7 % even for a relatively coarse resolution.