Research Summary Report of B04

[26.08.2023]

Ekanayaka, Virama; Doctoral researcher, v.ekanayaka@tu-braunschweig.de, TU Braunschweig, Institute of Machine Tools and Production Technology (IWF)

Hürkamp, André; Project Leader, a.huerkamp@tu-braunschweig.de, TU Braunschweig, Institute of Machine Tools and Production Technology (IWF)

Main goal

The integration of robot-guided additive manufacturing in the construction industry increases the degree of automation and can thus lead to an increased productivity and increased component quality. In shotcrete 3D printing (SC3DP), reproducible manufacturing results and ensuring component quality are major challenges, as the properties of shotcrete depend on many different parameters (e.g. temperature, pressure, water-cement ratio, hardening accelerator). The goal of this research project is to develop a reproducible, robot-guided shotcrete process based on multi-model adaptive path planning for the production of large, high-quality and complex components.

Summary

In order to ensure an accurate fabrication of the intended geometry, the implementation of an efficient process control during the SC3DP process is required. To establish the optimal process parameters such as nozzle velocity, distance to the printing surface, etc., a comprehensive understanding of the material-process interactions is essential. These interactions, crucial for both the stability and geometry of the printed structure, can be effectively explored through finite element simulations.

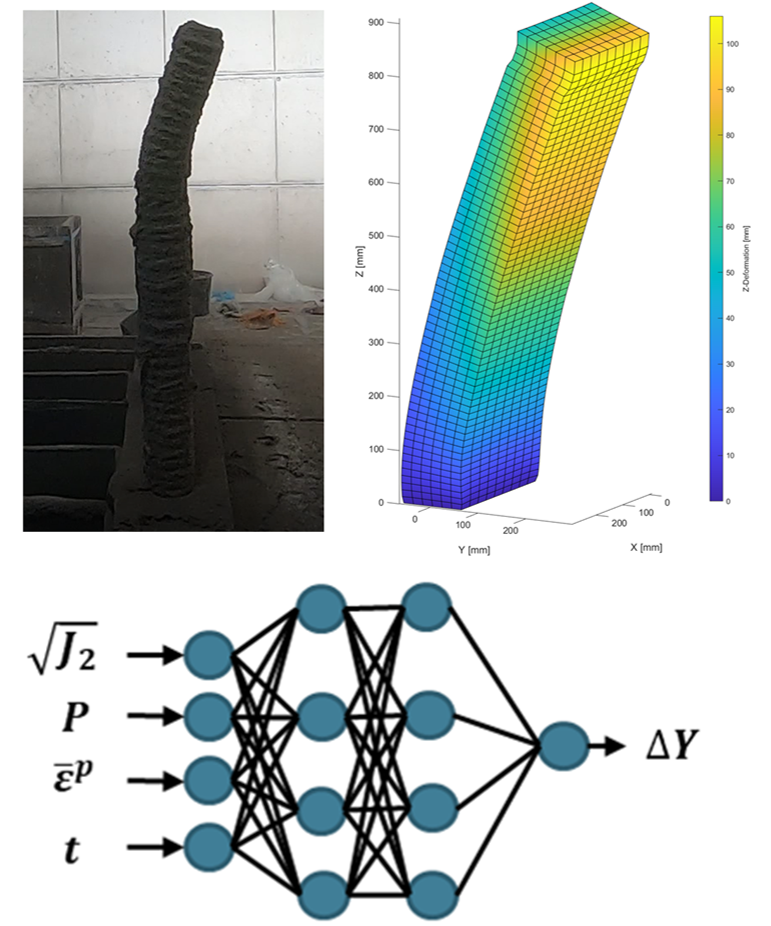
To achieve this goal a novel process-based finite element simulation has been developed within the framework of the B04 project, improving the conventional practice of using a designated CAD geometry and instead using the process parameters and printing trajectory. The time-dependent material properties of concrete has been numerically captured by assigning a time stamp to each mesh element, representing the moment it was printed. This enables the calculation of the corresponding material properties for each element at different time steps during the simulation simply by calculating the elapsed time. Consequently, the simulation’s output, including deformations and stress, is directly linked to these process parameters. This direct correlation allows for efficient fine-tuning of these parameters to achieve the desired outcomes.

The finite element simulations are however computationally expensive due to numerical iterations and the current state of research deals with speeding up the simulations, by replacing the conventional iterative processes with physics-based neural networks as shown in figure 1.

Current state of research

Numerical iterations which slow down the FE-simulation occur at two different stages. The equilibrium equation is iteratively solved using the Newton-Raphson method, and afterwards, during the material model stage of the simulation, the plastic multiplier is also calculated iteratively using the same procedure. To determine the plastic multiplier  in the strain-softening Drucker-Prager plasticity model, the following non-linear consistency equation must be solved.

Figure 2 illustrates how a physics based neural network was implemented in order to calculate the plastic multiplier  directly without using numerical iterations.

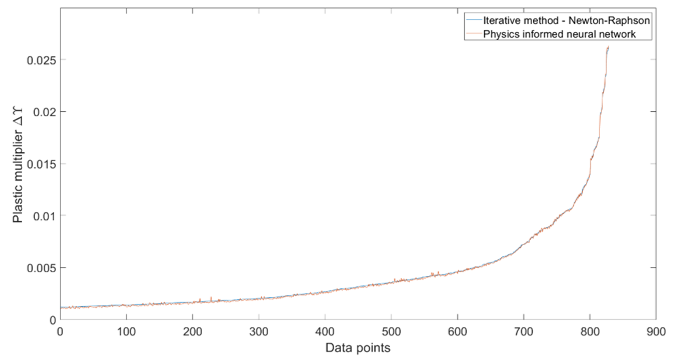
In physics based neural networks the underlying physical equation is directly encoded into the network and is trained at collocation points instead of using a traditional labelled data set. To generate the input data (data at collocation points), a single finite element simulation was carried out and the material data used to numerically compute  was saved. Then combinations of these parameters were generated using Latin Hypercube Sampling and the consistency equation shown above was solved at these combinations in the loss function of the neural network. After training the physics based neural network its performance was compared to numerically computed values as shown in figure 3.

The average percentage difference between the numerically determined value and through the neural network determined value was 5.13%, which demonstrates the effectiveness of the implemented network.