Research Summary Report C01

Bridging Scales – From Geometric Part Details to Construction Elements

Kollmannsberger, Stefan; PL, stefan.kollmannsberger@tum.de, TUM, CMS

Rank, Ernst; PL, ernst.rank@tum.de, TUM, Institute for Advanced Study

Oztoprak, Oguz; WiMi, oguz.oztoprak@tum.de, TUM, CMS

Digital models for Additive Manufacturing (AM) must consider many different geometric scales. The scales range from micrometers up to tens of meters for metal- or concrete-based processes. The TP C01 aims to develop consistent geometric and computational descriptions for the relevant AM products on all of these scales. Based on the multiscale geometric models developed in earlier phases of this research project, we are now focusing on efficient simulation methods for AM products in construction with special emphasis on validation of the developed techniques.

Summary

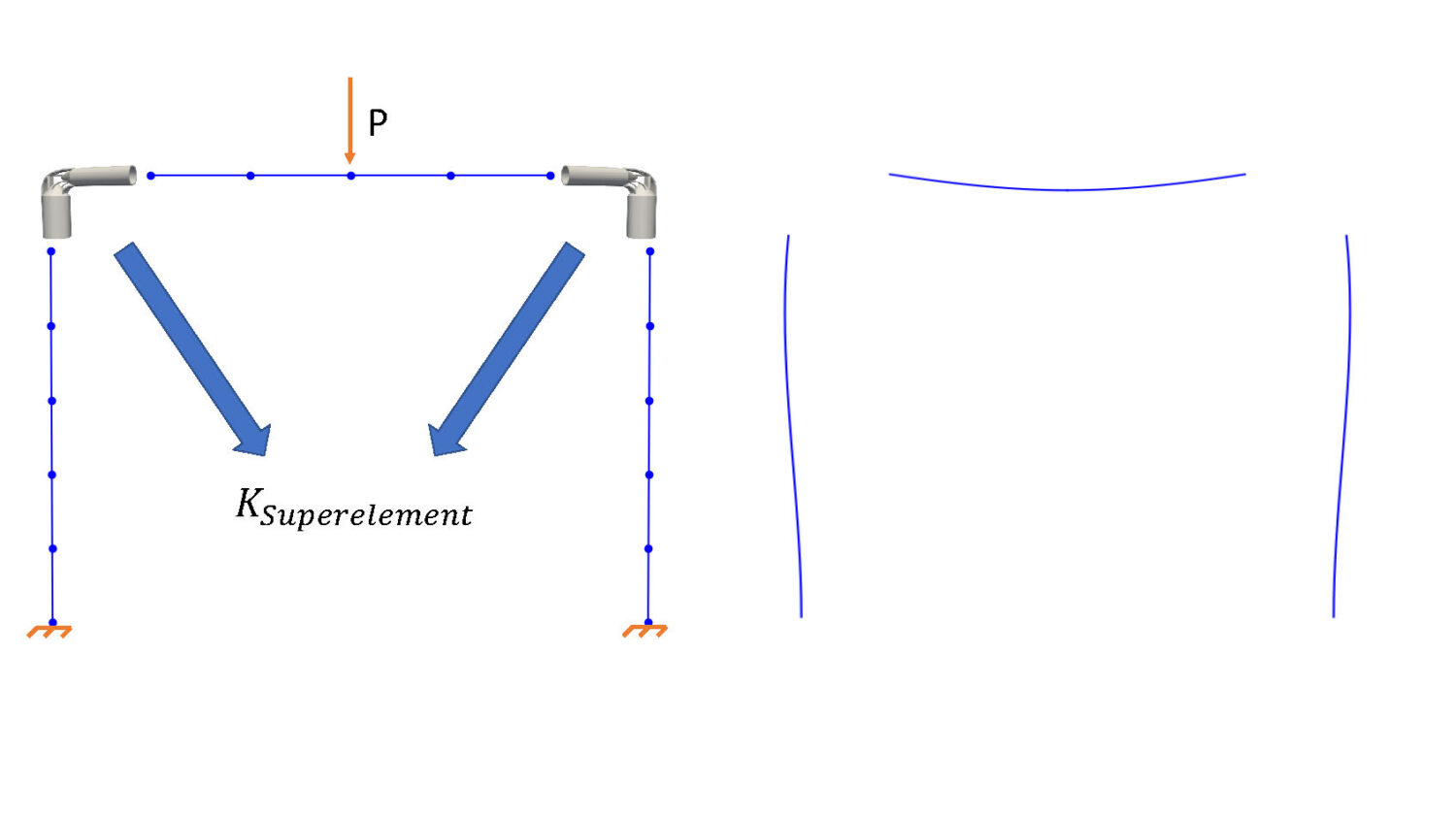
The advances in additive manufacturing facilitates the design of complex structural components. Structural nodes represent an example of such components that are of high practical relevance, e.g. space frames are composed of beams and connecting nodes. The complete set of geometric features inherent to the nodes can’t, in general, be represented during an efficient structural analysis on the construction scale. On the other hand, an accurate structural analysis on the construction scale must include macroscopic quantities representing the geometric details of such complex nodes. To this end, we are developing multiscale computational models that can represent nodes of arbitrary geometry in construction scale analysis.

Current state of research

To resolve the geometric complexity of complex nodes (e.g. Fig 1) in the global,  construction scale simulation, we develop a multiscale methodology based on ideas from reduced order modeling, substructuring and finite cell method. We consider the case where the space frames are modeled with beam elements.  First, the relevant macroscopic quantities associated with the connecting nodes are computed by utilizing the finite cell method for a 3D fully resolved analysis (Fig 1a-b). We then assemble and solve the global system with the nodes represented as superelements. Finally, the global solution (Fig 2b) is applied back on the local node where the behavior of the complex node under realistic loading conditions is analyzed (Fig 1c). This approach shines when the nodes are parametrically designed which lead to topological changes where the finite cell method can automatically compute the superelement matrices.