Research Summary Report of C02

M. Sc. Philipp Jakobs                            Researcher, philipp.jakobs@tum.de

Prof. Dr.-Ing. Roland Wüchner         Project leader, wuechner@tum.de

all: TU Munich (TUM), Chair of Structural Analysis

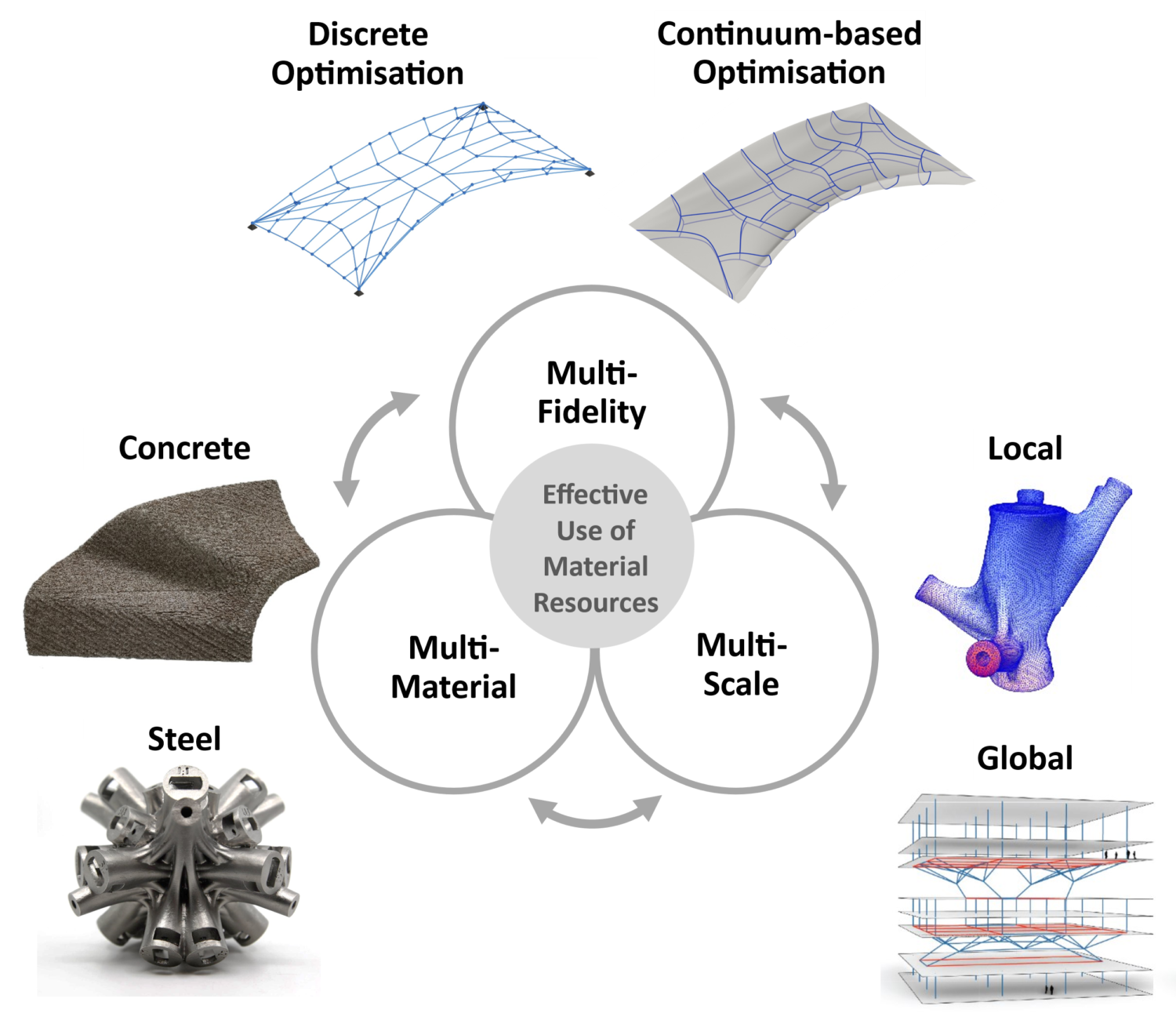
Current building practices often adopt a sequential design approach, where architectural, structural, and fabrication aspects are addressed independently, resulting in excessive material consumption. The CO2 project aims to establish a Holistic Design Framework (HDF) integrating the above-mentioned aspects. Within this framework, additive manufacturing facilitates structural optimisation by enabling the production of bespoke geometries for an effective use of material resources. Departing from the conventional sequential approach, the HDF concurrently integrates low-fidelity Discrete Optimisation Approaches and high-fidelity Continuum-based Optimisation Approaches (multi-fidelity). The HDF tackles a range of additive manufacturing processes by operating across different scales (multi-scale) and accommodating diverse materials (multi-material).

Summary

The CO2 project “3D Structural Puzzle”, initially focusing on small-scale structural optimisation for additive manufacturing, will now evolve into a Holistic Design Framework (HDF) for Additive Manufacturing in Construction. This hybrid framework enhances material efficiency in additive manufacturing by iterating through a structured workflow employing a multi-fidelity, multi-scale, and multi-material approach (Fig. 1). During the first months of the second funding period, the focus has been to further develop the existing methods of Continuum-based Optimisation Approach (COA) within the research group of PL Wüchner. In parallel, the working group of PL d’Acunto has worked on the extension of the Discrete Optimisation Approach (DOA) and its integration into one workflow with the COA, allowing bidirectional exchange between methods.

At the same time, first steps for the integration of AM specific constraints and objectives have already been taken. In cooperation with A01, A02, A06, A07 and A09 already first information about printable dimensions, material properties and possible anisotropic material behaviour has been exchanged. Once the DOA and COA are integrated into one holistic design framework, this data will be categorised into design variable-related and primal-related objectives and constraints and afterwards integrated into the framework.

Current state of research

At the moment, a constant refinement and extension of the existing methods for continuous optimisation methods is being pursued. In current research, the vertex morphing filtering was developed purely for geometrical design variables, e.g. shape, thickness and topology. For generalization this needs to be extended to arbitrary design variables in structural optimisation. To realise the multi-material aspect, a phase field formulation of the material density and young’s modulus can be formulated. The first steps for this have already been implemented into the OptimizationApplication in KratosMultiphysics. A simultaneous shape and multi-material optimisation (using two dummy materials) of an arch structure is displayed in Fig. 2.

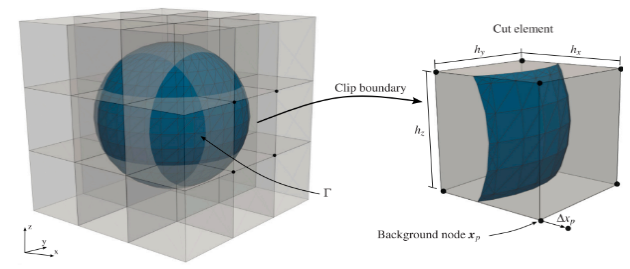
On the other hand, the interweaving of the COA and the DOA has to be established. An important milestone for that was achieved by Meßmer et al. with the development of a quadrature scheme of embedded solids (QuESo) [1] and the application of that technique in combination with vertex morphing [2]. This will be a helpful step to translate the form-found structure described by an STL file into a FEM model (see Fig. 3) that can be directly used for the COA techniques.

Current publications

1 – Meßmer, M., Najian Asl, R., Kollmannsberger, S., Wüchner, R., & Bletzinger, K. U. (2024). Shape optimization of embedded solids using implicit Vertex-Morphing. Computer Methods in Applied Mechanics and Engineering, 426. https://doi.org/10.1016/j.cma.2024.116999