Research Summary Report of B03

Prof. Dr. rer. nat. M. Geier              Project leader, geier@irmb.tu-bs.de

Dr.-Ing. K. Kutscher                         Researcher, kutscher@irmb.tu-bs.de

Prof. Dr.-Ing. habil. M. Krafczyk   Project leader, kraft@irmb.tu-bs.de

Dr.-Ing. H. Alihussein                      Researcher, hussein@irmb.tu-bs.de

All: TU Braunschweig, Institute for Computational Modeling in Civil Engineering, IRMB (Institut für rechnergestützte Modellierung im Bauingenieurwesen)

The project is currently concerned with the simulation of a moving nozzle for the injection process using I3DCP. We are particularly interested in the influence of the movement of the nozzle on the printed strand.

Summary

The I3DCP is a three-phase problem where the deposited concrete and the suspension fluid have to be modelled together with the solid nozzle of the printer. The two fluids are distinguished by phase field that is advected with the velocity field. As the domain is discretized with an Eulerian grid, the movement of the solid nozzle requires permanent remeshing and reinitialization of new grid nodes. In order to accelerate the remeshing the solid part is modelled as an implicit body that can be evaluated quickly.

Reinitialization of the phase field in the wake of the moving nozzle leads to a violation of mass conservation. By combining sharp boundary conditions for the momentum equation with an immersed boundary method for the phase field this problem could be overcome.

Current state of research

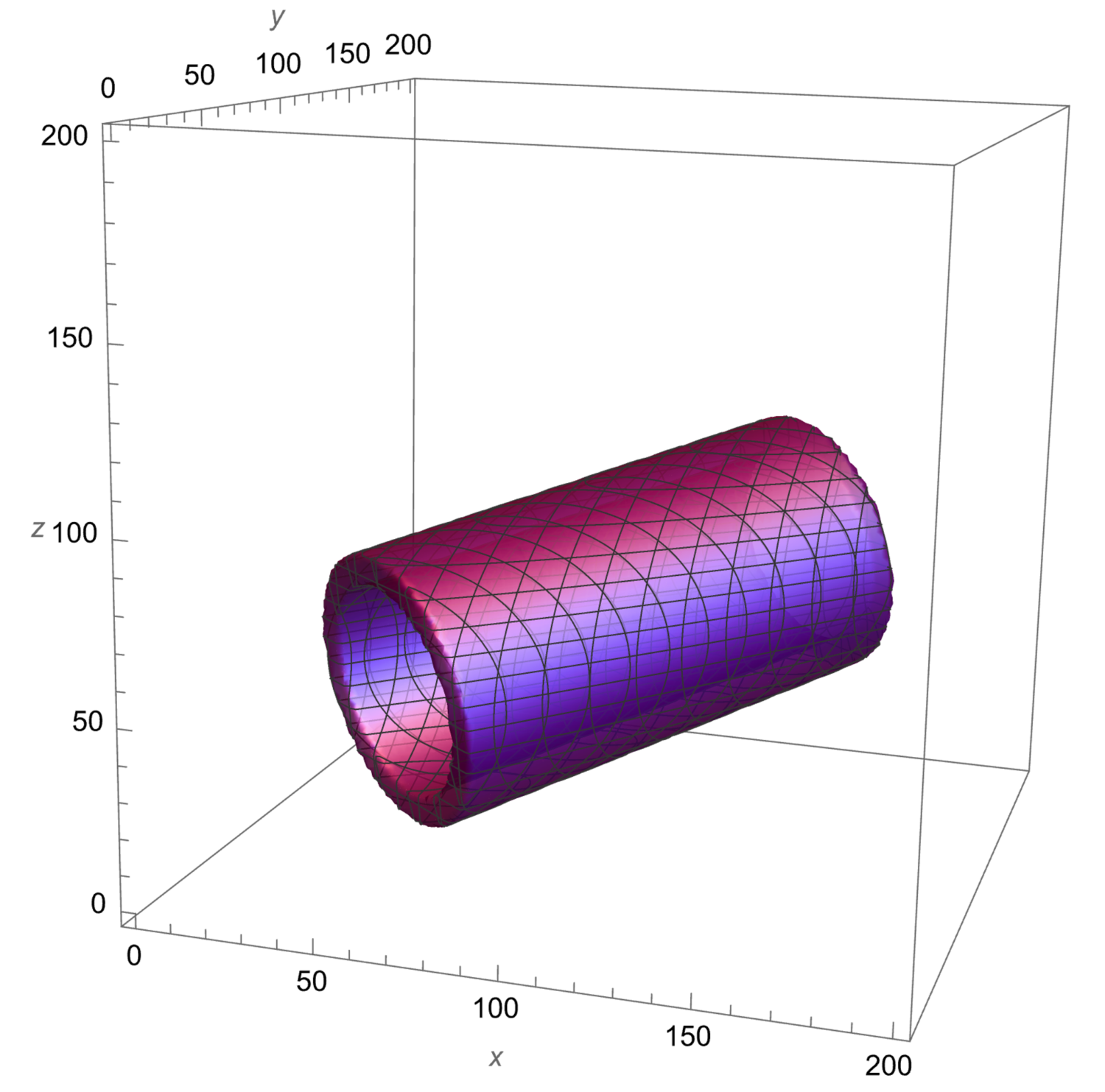
Due to the relatively low density ratio between the liquid concrete and the carrier fluid in the I3DCP process the interaction between the two fluids can be simulated by a velocity pressure formulation smooth interface model. The phase indicator  determines whether a point is inside the concrete phase () or the carrier phase (). The nozzle represents a third solid phase. Stationary solid objects are usually modeled with zero penetration boundary conditions. Mobile solid objects require repeated remeshing, the consideration of the object’s local velocity in the boundary method, and the initialization of new collocation points that were previously covered by the solid. Remeshing typically is a rather expensive operation. Solid objects are usually represented by triangle meshes. Determining whether a point is inside or outside the solid requires a complicated ray trancing procedure that counts how often a beam from the point to a known outside points cuts through one of the triangles. If the number of cuts is odd, the point is inside, otherwise it is outside. As this procedure takes up a considerable amount of compute time and has to be repeated in every time step if the body is moving, we developed a much quicker way to determine whether a point is inside or outside the nozzle. Instead of using a triangle representation, the nozzle was modelled with a customized implicit function . Similar to the phase field equation, a point is determined to be outside the body if   and inside otherwise. Figure 1 shows the rendering of the pipe used as a model for the nozzle.

Both the momentum equation and the phase field equation are solved with a lattice Boltzmann method based on discrete distribution functions as primary variables. Newly uncovered lattice nodes require a reinitialization of the distribution function. This can be done in different ways. For the momentum equation, an initialization with an equilibrium distribution is usually sufficient. The equilibrium is a function of the local velocity and the pressure and can be easily determined given the velocity of the solid object. However, the equilibrium function for the phase field also depends on the location of the surface of the homogenized phase interface. Attempts to interpolate the phase field lead to a violation of the conservation of mass, as the mass would only be conserved if the integral over   remained constant. Imposing this on the domain leads to a global balance problem that would break the efficiency of the lattice Boltzmann method. To circumvent this difficulty, we decided to implement a method that does not require reinitialization of the phase field distribution function.

The phase field equation is an advection-diffusion-anti-diffusion equation. The anti-diffusion is tailored to counteract the diffusion of a predefined hyperbolic tangent profile for the phase indicator. This counterbalance is imposed to keep the three-dimensional shape of the phase interface constant. Deformations of the phase interface are only induced by the advection of the phase field with the velocity obtained from the solution of the momentum equation. By reinitializing the momentum equation at all internal nodes in the solid with the velocity of the solid, the velocity field for the advection of the phase indicator can be extended to the inside of the solid body. As the nozzle undergoes solid body movements only, the velocity field inside is homogenous and free from deformations such that the phase indicator field is not deformed inside the solid either. In this way the implementation of boundary conditions and reinitialization for the phase indicator is avoided.